Hello friends, I hope you have been having a great and refreshing time during this holiday season. In my last article I talked about linear models, the intuition behind them using the sklearn module. What better way to start the year than to give a brief introduction to Linear Support Vector Machines? I would like to brief you of the intuition and logic behind it as well as show you how to implement it using scikit-learn.
The support vector machine is a non-probabilistic (supervised machine learning) binary classifier which classifies data labels by means of a separating line known as a hyperplane while maximizing a set distance known as the margin from data instances (support vectors) of each class. They are originally known as linear classifiers but they can also by used for performing non-linear classification using what is known as the kernel trick. The high versatility of the support vector machine also makes it suitable for performing regression and clustering operations. This article focuses more on linear support vector classifier and would only treat the kernel trick just as an honorable mention.
The optimal hyperplane which separates the class labels is usually defined as satisfying the function in eqn i.
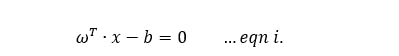Therefore, in the case of binary classifiers, we seek to find two margins such as in eqn ii. whereby the sign indicates what class a features vector or data instance would fall into.
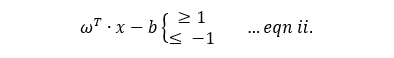
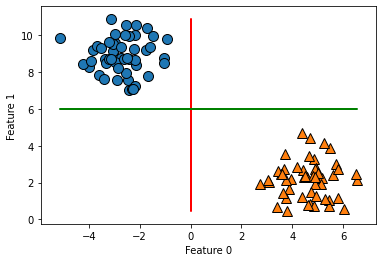
Let’s consider the plot of hypothetical hyperplanes of the SVM for a binary class labelled dataset below. It can be seen that although these lines cut through the different classes quite well, none of these is either optimally splitting both labels or is giving us the maximum margin from the line to the support vectors of each class label.
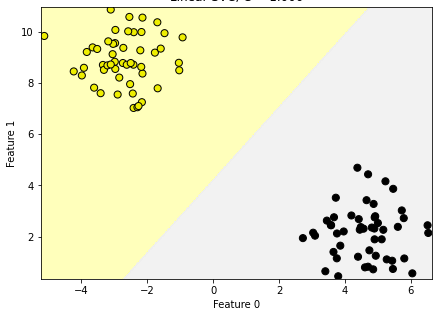
Next, we consider the plot showing the optimal hyperplane which provides us with the maximum margin for the same dataset. Our optimal hyperplane is said to satisfy eqn i. and our fitted model would satisfy either of the given constraint in eqn ii. `
Time to see how to implement this using the scikit-learn module.
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.datasets import make_blobs
>>> X,y = make_blobs(centers = 2, random_state = 42)
>>> y = y%2
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)
>>> from sklearn.svm import LinearSVC
>>> clf = LinearSVC().fit(X_train, y_train)
>>> print("Performance of the SVC on test data:", clf.score(X_test, y_test))
Performance of the SVC on test data: 1
Whaaat?!! Our model has an 100% accuracy! Its unfortunate though that real life dataset would not always look this direct and might look like this
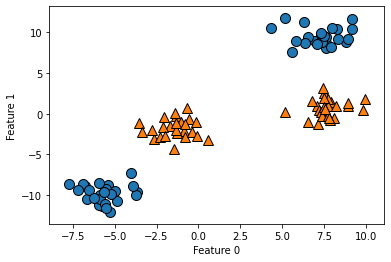Or maybe more clustered than this. It then gets difficult to easily separate these classes by a straight line. But what if we can transform our dataset in such a way that makes it easy for us to separate these classes like
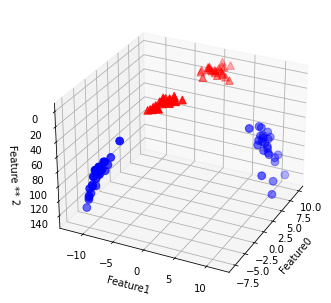The kernel trick (honourable mention…haha) makes this possible. The scope of this article won’t cover that but I hope you have learnt something from what we have covered on Linear Support vector machines. I have attached some extra resources from which you could read up to get some knowledge on kernel tricks and methods.
If you have any questions, comments or additions, feel free to make a comment below. Thanks for reading and I wish us all a productive and goal-smashing 2021 ahead. Cheers!